気体の状態方程式はPV=nRT~
気体の状態方程式はPV=nRTです。
Pは圧力
Vは体積
nは物質量
Rは定数(ある数字 という意味)(気体定数)
Tは温度
気体は小さすぎて目に見えませんが、小さな粒子です。
小さな粒子なので、ものにぶつかります。
そのときに発生するのが圧力Pです。
気体の状態方程式を考える仮想実験
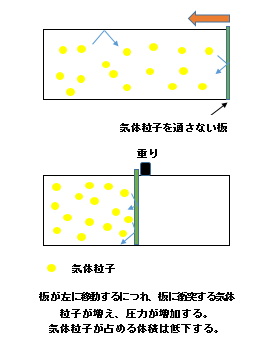
ここで仮想実験をしましょう。
箱の中にある気体が入っている
隙間が全くない穴も開いていない動く板が右端にあります。
動く板をど真ん中に置くのには、力が必要です。
そのときに空気の方から押される力が圧力Pです。
左側の体積がVになります。
空気の量(物質量)をnとすると空気の温度Tに対して
PV=nRT
という関係が成り立ちます。
この式を「気体の状態方程式」といいます。
温度Tは運動エネルギーに比例するので、温度が上がると、気体粒子の運動も激しくなり、圧力Pや体積Vが上がるのはイメージできると思います。
また気体粒子の量が多いと、圧力Pや体積Vが上がるのもイメージできるでしょう。
以下は余裕がある人が読み進めてください。↓
ボイルの法則 PV=k(Tは一定の条件下)
仮想実験のなかで
動く板をVが半分になるまで動かしましょう。
すると、気体粒子の衝突する回数はその分だけ増えるのが分かると思います。
つまりPV=k(定数)
というわけです。
シャルルの法則V=k’T(Pは一定の条件下)
箱の真ん中で板を固定するために重りを乗っけておきます。
気体の入った左側だけを熱すると、温度Tが上がります。
Tは運動エネルギーに比例するので、気体は動き回り、抑えられていた板がすこしずつ右に動き、Vが増えるのはイメージできると思います。
これがシャルルの法則 V=k’Tです。(k’は定数)
ボイル・シャルの法則 PV/T=k”
圧力P₁ 体積V₁ 温度T₁のものをP₃ V₃ T₃に変化させます。
まず圧力一定のまま、温度をT₂に熱すると
$$\frac{V₁}{T₁}=\frac{V₂}{T₂}(シャルルの法則より)$$
これより $$ V₂= \frac{V₁T₂}{T₁} (温度が上がった分だけ体積が広がる) $$
次に
温度をT₂のまま圧力P₃ 体積V₃にすると
P₂V₂=P₃V₃(ボイルの法則より)
P₁=P₂ T₂=T₃なので、これより
PV/T=一定を導きたいのでP₁ V₁ T₁をP₃ V₃ T₃であらわすのを目指す
P₁V₁/T₁=P₁V₂/T₂= P₂V₂/T₂ =P₃V₃/V₂×V₂/T₂=P₃V₃/T₂=P₃V₃/T₃
つまり(P₁ V₁ T₁)⇒(P₃ V₃ T₃)と変化してもPV/Tは一定である。
PV=nRT
ボイルシャルルの法則よりPV/T=k”
この定数k”は、物質量モルに比例するのはイメージがつくと思います。
(量が増えた分だけ衝突の回数や体積は増える)
つまりK”=nR (Rは気体定数という)
つまりPV=nRTというわけです。





